A discovery of what lies beyond mathematics, looking past the usual stereotypical views that many people have, sharing the thoughts of a student studying mathematics.
25 October 2012
Trigonometry Series (Part 2)
There are several important angles which are often found very useful when working with trigonometric functions. Let's take a look at these:
(From: http://www.analyzemath.com)
In the table 'U' means that it is undefined, since we cannot divide by zero.
Remember the relationship between sin and cosec, cos and sec, tan and cot, then you'll see how to use this table for all six functions.
There are two important triangles that we can make use of to easily calculate these "speccial" angles:
(From: http://prepfortests.com)
Also, we can make use of the unit circle to calculate some other special angles:
(From: http://etc.usf.edu)
In conclusion, knowing the two triangles and the unit circles gives you all the information of the table and then you never need to remember the values of any angles.
Next time we take a look at some identities and laws.
(From: http://www.analyzemath.com)
In the table 'U' means that it is undefined, since we cannot divide by zero.
Remember the relationship between sin and cosec, cos and sec, tan and cot, then you'll see how to use this table for all six functions.
There are two important triangles that we can make use of to easily calculate these "speccial" angles:
(From: http://prepfortests.com)
Also, we can make use of the unit circle to calculate some other special angles:
(From: http://etc.usf.edu)
In conclusion, knowing the two triangles and the unit circles gives you all the information of the table and then you never need to remember the values of any angles.
Next time we take a look at some identities and laws.
24 October 2012
Trigonometry Series (Part 1)
Welcome to the first part of my trigonometric series. I will discuss all the basic knowledge you need to have concerning trigonometric functions and end the series with some examples and problems.
Consider a right-angled triangle
(Right-angled means that there is an angle which is 90 degrees, or π/2.)
We define the trigonometric functions as follow

together with

We will almost always make use of right-angled triangles when working with trigonometric functions because of the way that they are defined.
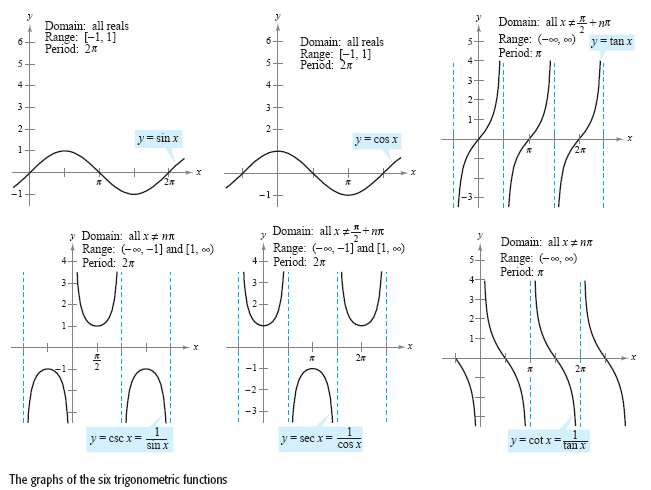
Graphs:
(Graphs from: http://www.algebra-help.org)
Next time I will discuss some important angles.
Consider a right-angled triangle
(Right-angled means that there is an angle which is 90 degrees, or π/2.)
We define the trigonometric functions as follow
together with
We will almost always make use of right-angled triangles when working with trigonometric functions because of the way that they are defined.
Graphs:
(Graphs from: http://www.algebra-help.org)
Next time I will discuss some important angles.
23 October 2012
The absolute value
The absolute value function is used to indicate length and one important property that is used here is that length is always positive.
Let's consider a few examples:
|23| = 23
|-7| = 7
The definition of an absolute value is:
|a| = a if a > 0
or
|a| = -a if a < 0
where a can be any number and trivially
|0| = 0.
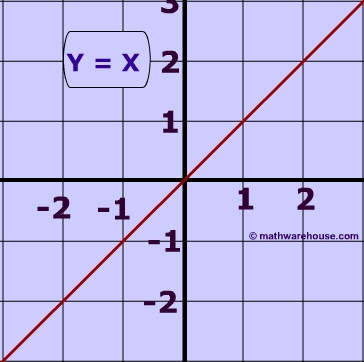
The equation of a trivial straight line is y = x. This is a line going through the origin and where the gradient is 1. If we now want to draw the function y = |x|, how will it be different from this straight line?
Well there is only one difference and that is that all the function values must be positive. Let me explain this by means of graphs.
This is the graph of the straight line
and this is the graph of the absolute value y = |x|.
(image from: http://hotmath.com)
Do you see what has happened?
The negative part of the line just became positive, so i.e. if y = -2 for the line, then y = 2 for the absolute value function.
| Stay positive! |
Let's consider a few examples:
|23| = 23
|-7| = 7
The definition of an absolute value is:
|a| = a if a > 0
or
|a| = -a if a < 0
where a can be any number and trivially
|0| = 0.
The equation of a trivial straight line is y = x. This is a line going through the origin and where the gradient is 1. If we now want to draw the function y = |x|, how will it be different from this straight line?
Well there is only one difference and that is that all the function values must be positive. Let me explain this by means of graphs.
This is the graph of the straight line
and this is the graph of the absolute value y = |x|.
(image from: http://hotmath.com)
Do you see what has happened?
The negative part of the line just became positive, so i.e. if y = -2 for the line, then y = 2 for the absolute value function.
| Stay positive! |
22 October 2012
Logarithms
Following the relation with exponential functions, I had to include some explanation of the logarithmic functions.
As we have seen before, if

then

Here follows the properties:




and we also have the special case

which we call the ln (pronounced "lin") function which is also called the natural logarithm and is the inverse of the natural exponential function which is the function e.

All of these properties can be proven by making use of the relation between them and the exponential functions (the fact that they are inverses of each other) and the properties of the exponential functions.
As we have seen before, if
then
Here follows the properties:
and we also have the special case
which we call the ln (pronounced "lin") function which is also called the natural logarithm and is the inverse of the natural exponential function which is the function e.
All of these properties can be proven by making use of the relation between them and the exponential functions (the fact that they are inverses of each other) and the properties of the exponential functions.
Subscribe to:
Posts (Atom)