Trigonometry Series (Part 3)

The following identities come in very useful when we are solving equations of trigonometric functions.

This is the basic identity

and these two can be derived from the first identity


taking note that



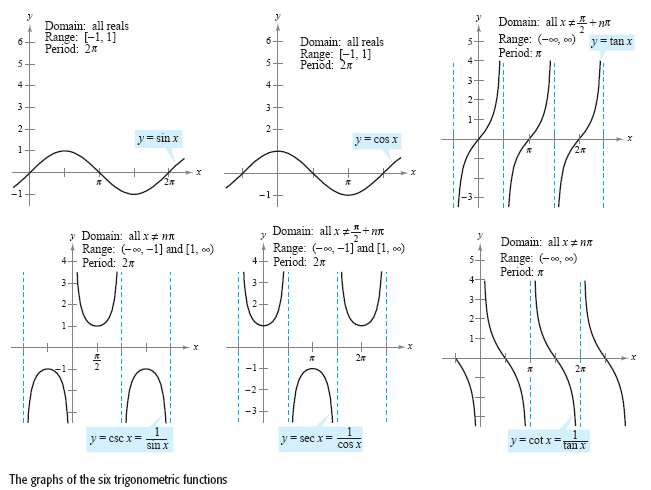
These following angle-identities can easily be derived if we take a look at the graphs of he respectively functions (see Trigonometry Series (Part 1)).






Consider any triangle, it need not be right-angled,



then there are two laws that can help us to calculate angles or side length of a triangle, given that we have the information about three other angles and/or sides of the triangle.
 
Law of Sines

 

Law of Cosines:



Next time we take a look at some useful formulas.

Divided by Zero

Trigonometry Series (Part 2)

There are several important angles which are often found very useful when working with trigonometric functions. Let's take a look at these:

(From: http://www.analyzemath.com)

In the table 'U' means that it is undefined, since we cannot divide by zero.

Remember the relationship between sin and cosec, cos and sec, tan and cot, then you'll see how to use this table for all six functions.

There are two important triangles that we can make use of to easily calculate these "speccial" angles:

(From: http://prepfortests.com)


Also, we can make use of the unit circle to calculate some other special angles:

 (From: http://etc.usf.edu)

In conclusion, knowing the two triangles and the unit circles gives you all the information of the table and then you never need to remember the values of any angles.

Next time we take a look at some identities and laws.

Trigonometry Series (Part 1)

Welcome to the first part of my trigonometric series. I will discuss all the basic knowledge you need to have concerning trigonometric functions and end the series with some examples and problems.

Consider a right-angled triangle

(Right-angled means that there is an angle which is 90 degrees, or π/2.)

We define the trigonometric functions as follow




together with



We will almost always make use of right-angled triangles when working with trigonometric functions because of the way that they are defined.

Graphs:

(Graphs from: http://www.algebra-help.org)

Next time I will discuss some important angles.

The absolute value

The absolute value function is used to indicate length and one important property that is used here is that length is always positive.
Let's consider a few examples:
|23| = 23
|-7| = 7
The definition of an absolute value is:
|a| = a if a > 0
or
|a| = -a if a < 0
where a can be any number and trivially
|0| = 0.

The equation of a trivial straight line is y = x. This is a line going through the origin and where the gradient is 1. If we now want to draw the function y = |x|, how will it be different from this straight line?
Well there is only one difference and that is that all the function values must be positive. Let me explain this by means of graphs.
This is the graph of the straight line

and this is the graph of the absolute value y = |x|.

(image from: http://hotmath.com)

Do you see what has happened?
The negative part of the line just became positive, so i.e. if y = -2 for the line, then y = 2 for the absolute value function.

| Stay positive! |